7.4Уравнения с модулем

1.

2.

• СОДЕРЖАНИЕ
Понятие
модуля
Уравнения,
содержащие
переменную
под знаком модуля

3. Понятие модуля

Модулем числа а называется расстояние от начала
отсчета до точки с координатой а
| а|
а
0
Например:
|-7|=7
-7
Таким образом:
х
| 7 | =7
0
а, если а 0,
а
а, если а 0
7
х

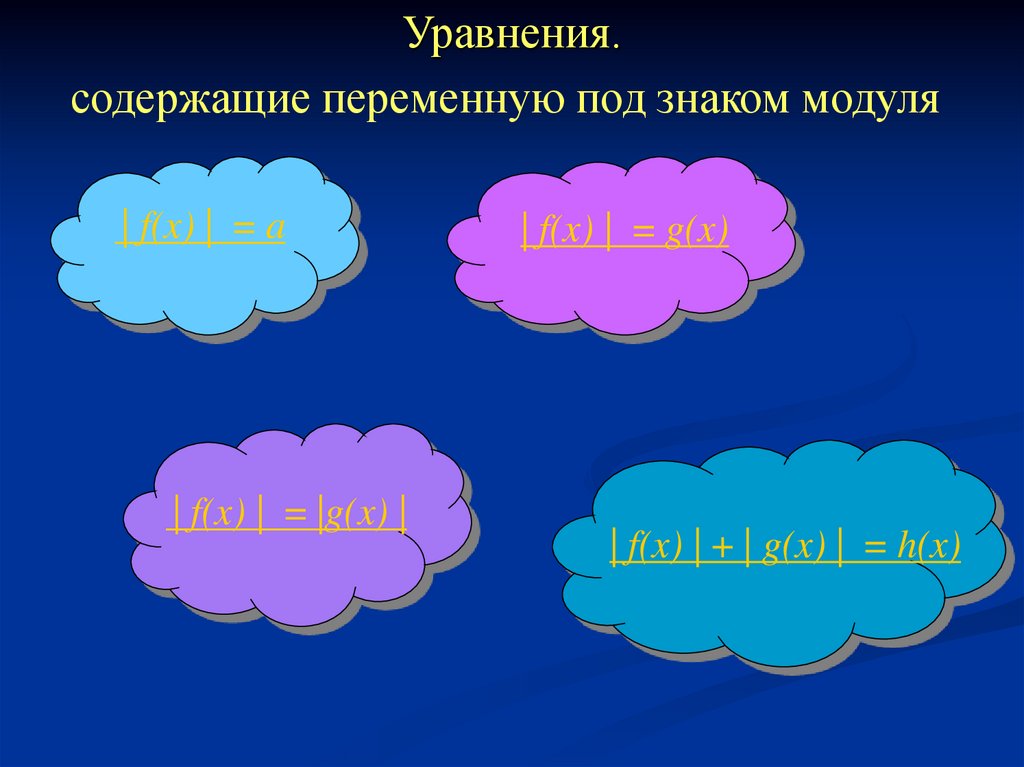
4. Уравнения.

содержащие переменную под знаком модуля
| f(x) | = a
| f(x) | = |g(x) |
| f(x) | = g(x)
| f(x) | + | g(x) | = h(x)

5. Уравнение вида | f(x) | = a

Если а < 0, то уравнение решений не имеет
Если а = 0, то f(x) = 0
Если а > 0, то f(x) = а или f(x) = - а
Пример:
Решить уравнение: | 2х – 5 | = 13
Решение: 2х – 5 = 13 или 2х – 5 = - 13
2х = 13 + 5
2х = - 13 + 5
2х = 18
2х = - 8
х =9
х = -4
Ответ: х = 9 , х = - 4

6. Уравнение вида | f(x) | = a

Решите уравнение
• 1) | 2х - 3| = 7
• 2) .|х2 – х - 5| = 1
• 3) | |x| - 2 |= 2

7. Уравнение вида | f(x) | = g(x)

• 1) определить условие, при котором уравнение имеет решение:
g(x) ≥ 0
• 2) f(x) = g(x) или f(x) = - g(x)
• 3) Решить уравнения и выбрать корни, удовлетворяющие
условиюg(x) ≥ 0
• Пример: Решить уравнение:| х + 2| = 2( 3 – х)
• Определим при каких значениях х уравнение имеет решение
2( 3 – х) ≥ 0 => х ≤ 3
• Распишем данное уравнение на два:
х + 2 = 2( 3 – х) или х + 2 = - 2( 3 – х)
х = 4/3
х = 8 не удовлетворяет условию х ≤ 3
• Ответ: х = 4/3

8.

Уравнение вида | f(x) | = g(x)
Решите уравнения
1) |5х + 2| = 3 – 3х
2) |х2 - 2х| = 3 - 2х

9. Уравнение вида | f(x) | = | g(x)|

1способ: f(x) = g(x) или f(x) = - g(x)
2способ: возвести обе части уравнения в квадрат
Пример Решить уравнение: |х + 2| = |2х - 6|
1 способ: х + 2 = 2х – 6 или х + 2 = - (2х – 6)
х = 8
3х = 4
х = 4/3
2 способ: (|х + 2|)2 = (|2х - 6|)2 Воспользуемся свойством |а|2=а2
(х + 2)2 = (2х - 6)2
3х2 – 28х + 32 = 0 => х = 8, х = 4/3

10.

Уравнение вида | f(x) | = |g(x)|
Решите уравнения
1) |х2 + х - 2| = |х +2|
2) |3 + х |= |х|

11. Уравнение вида | f(x) | + | g(x)| = h(x)

• При решении уравнений данного вида используется
правило раскрытия модуля.
• Пример: Решить уравнение:|х-3| + |2х-1| =8
1
• Найдем нули функций, стоящих под знаком модуля: х= 3, х= 2
• Отметим эти точки на числовой прямой и определим знаки функций на
получившихся промежутках
1
2
3
х 3
2х 1
Рассмотрим решение уравнения на каждом промежутке
1
х
2
1
х 3
2
х 3

12. Уравнение вида | f(x) | + | g(x)| = h(x)

• Пример: Решить уравнение: |х-3| + |2х-1| =8
х
1
1 2
3
х 3
2х 1
2
Раскроем модули с учетом знака функций на этом промежутке
- ( х-3 ) – ( 2х-1 ) = 8
- 3х +4 = 8
1
4
х
удовлетворяет условию
х
2
3

13. Уравнение вида | f(x) | + | g(x)| = h(x)

Пример: Решить уравнение:|х-3| + |2х-1| =8
1
2
3
х 3
2х 1
1
х 3
2
Раскроим модули с учетом знака функций на этом промежутке
- ( х-3 ) + ( 2х-1 ) = 8
х+2=8
х=6 не удовлетворяет условию 1 х 3
2

14. Уравнение вида | f(x) | + | g(x)| = h(x)

Пример: Решить уравнение:|х-3| + |2х-1| =8
1
2
3
х 3
х 3
2х 1
• Раскроем модули с учетом знака функций на этом
промежутке
( х-3 ) + ( 2х-1 ) = 8
3х - 4 = 8
х=4 удовлетворяет условию х 3

15. Уравнение вида | f(x) | + | g(x)| = h(x)

Объединим все ответы
1
2
1
х
2
х
4
3
3
х 3
2х 1
1
х 3
2
х 3
решений нет
х 4
Ответ: х
4
3
х 4

16. Уравнение вида | f(x) | + | g(x)| = h(x)

Решите уравнения
2 х 3 х 1 2х 1
3 х 3 х 5 2х
х 2 х 2 2х